Inviscid fluids are governed by the Euler equations, which are a statement of conservation of mass, momentum, and energy:

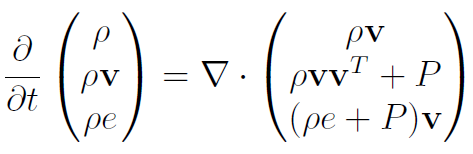
In addition, one typically assumes an equation of state (relationship between pressure and density) to close the system off, such as the ideal gas law:

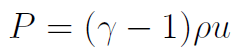
where the internal energy (u) and total energy (e = internal + kinetic) are related by:

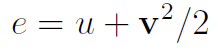
If you add magnetic fields and Maxwell’s equations (assuming no resistivity), you get the ideal MHD equations

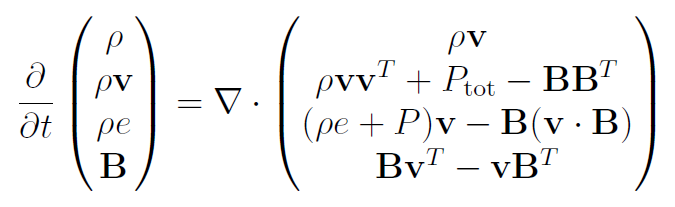
where the total pressure is a sum of the gas pressure and magnetic pressure:

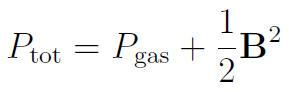
The above equations of fluid dynamics are partial differential equations, which means they only apply to smooth flows. Shocks, however, are discontinuities in the fluid variables (e.g. velocity, pressure):

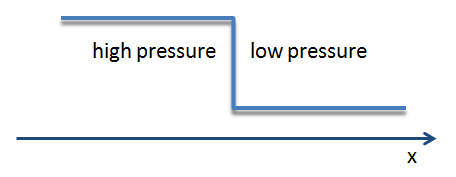
The fluid equations are incompatible at the shock discontinuity, because spatial derivatives are ill-defined.

To solve for shock structure, you need to satisfy the Rankine-Hugoniot jump conditions, which are just statements of conservation of mass, momentum, and energy. They are obtained by integrating the Euler/MHD equations across the discontinuity.

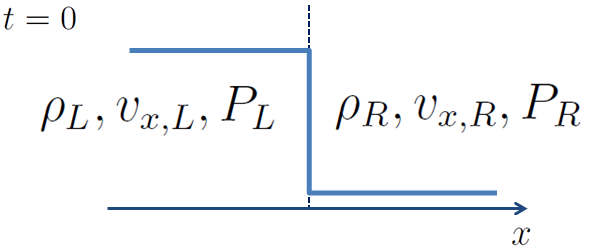
The 1D Riemann problem is a good way to understand shock basicsIt asks, how does a fluid evolve if I set up a discontinuity in density, velocity, and pressure at t=0?

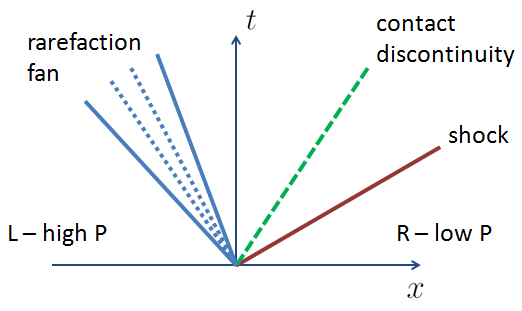
The shock structure is complex. You don’t simply get an advection of the discontinuity. You produce several waves.

In an Euler fluid, you have 3 characteristic velocities:

You obtain three types of features:

• Shock: sharp discontinuity in fluid variables, physically admissible only if there is an entropy increase through the shock
• Rarefaction fan: occurs instead of shock when there is no entropy increase through shock
• Contact discontinuity: discontinuity in density only. It advects passively.

You end up with characteristics that may look something like:

In the MHD equations, things get more complicated. You have 7 characteristic velocities (and they can sometimes be degenerate!)

You end up with characteristics that may look something like:

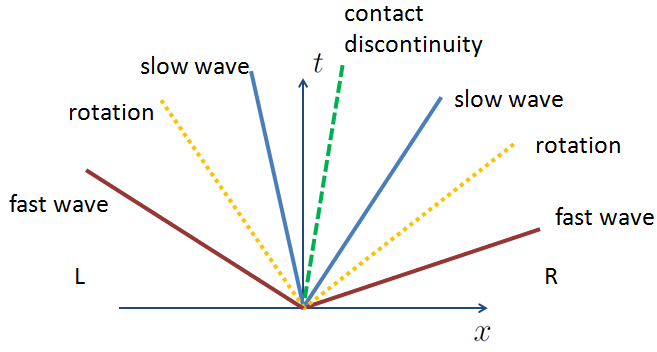
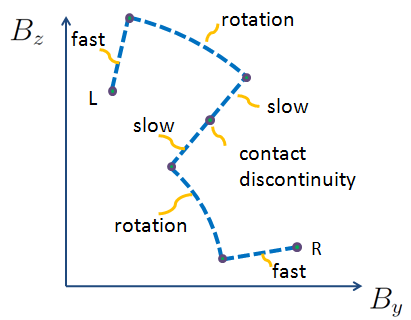
In MHD shocks, you obtain a new type of discontinuity:

• Rotational discontinuity: A rotation of the transversal magnetic field associated with the Alfven wave speed

~~~

This concludes the basic theory background. You can click on the Euler and MHD tabs on the top of the page to explore the shock structure in a interactive Mathematica module.